One of the major contributions Archimedes made to mathematics was his method for approximating the value of pi. It had long been recognized that the ratio of the circumference of a circle to its diameter was constant.
Archimedes’ Method in his book: Measurements of a Circle
1. The area of a circle is equal to that of a right-angled triangle where the sides including the right angle are respectively equal to the radius and circumference of the circle.
2. The ratio of the area of a circle to that of a square with side equal to the circle’s diameter is close to 11:14 which is equivalent to saying that pi is close to 22/7.
3. The ratio of the circumference of any circle to its diameter is less than 31⁄7 but greater than 310⁄71.
How?
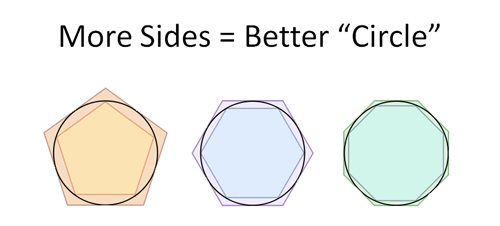
Archimedes used the method of exhaustion to approximate the value of pi. He did this by drawing a larger regular polygon outside of a circle and a smaller regular polygon inside the circle. Doubling the number of sides of each regular polygon and calculating the length of each side. As the number of sides increases, it becomes a more accurate approximation of a circle. Finally, when the polygon had 96 sides, he was able to determine that the value of pi lay between 31⁄7 and 310⁄71. The midpoint puts pi at 3.14159 which is over 99.999999% accurate.
Method of Exhaustion
The method of exhaustion is a method of finding area of a shape by inscribing polygons inside so that the area of the polygon would converge with the area of the shape.
Archimedes’ Method in his book: Measurements of a Circle
1. The area of a circle is equal to that of a right-angled triangle where the sides including the right angle are respectively equal to the radius and circumference of the circle.
2. The ratio of the area of a circle to that of a square with side equal to the circle’s diameter is close to 11:14 which is equivalent to saying that pi is close to 22/7.
3. The ratio of the circumference of any circle to its diameter is less than 31⁄7 but greater than 310⁄71.
How?
Archimedes used the method of exhaustion to approximate the value of pi. He did this by drawing a larger regular polygon outside of a circle and a smaller regular polygon inside the circle. Doubling the number of sides of each regular polygon and calculating the length of each side. As the number of sides increases, it becomes a more accurate approximation of a circle. Finally, when the polygon had 96 sides, he was able to determine that the value of pi lay between 31⁄7 and 310⁄71. The midpoint puts pi at 3.14159 which is over 99.999999% accurate.
Method of Exhaustion
The method of exhaustion is a method of finding area of a shape by inscribing polygons inside so that the area of the polygon would converge with the area of the shape.